Home / Research Notes / Note 2: Optimization-based Locomotion Planning, Estimation, and Control Design for the Atlas Humanoid Robot

Optimization-based Locomotion Planning, Estimation, and Control Design for the Atlas Humanoid Robot

by Scott Kuindersma, Robin Deits, et al, 2016, Paper Link

summarized by Peijie Xu

0. Abstract

This paper describes a collection of optimization algorithms for achieving dynamic planning, control, and state estimation for a bipedal robot.

Including footstep placement & whole-body planning and control

1 Introduction

2 Atlas

28 actuated DOF: 6 in each leg and arm, 3 in the back, and 1 neck joint

3 Motion Planning

Decompose the discrete phase into 2 parts

1. Analyze the environment and compute a set of convex regions where contacts are allowed.
2. Solve an optimization problem that assigns contacts to these regions in a way that minimizes cost while respecting kinematic and dynamic constraints.

Two approaches for assigning contacts to convex regions for different tasks

1. footstep planning
2. planning to grab handrails or transition from prone to standing

3.1 Footstep Planning as a Mixed-Integer Convex Problem

Represent the problem as single mixed-integer convex optimization, in which the number of footsteps and their positions and orientations are simultaneously optimized

Existing footstep planning methods: discrete searches and continuous optimizations. This work performs a simultaneous optimization of the discrete assignment of footsteps to convex regions and the continuous position of the footsteps within those regions.

Transform the problem of avoiding obstacles into a discrete problem of assigning each footstep to some convex region that is known to be obstacle-free

DEFINE

$P_1,P_2,...,P_N$$P_1,P_2,...,P_N$: the poses of the footsteps, expressed as position and yaw with $p_j=(x_j,y_j,z_j,{\theta }_j)$$p_j=(x_j,y_j,z_j,\theta_j)$

$G_1,G_2,...,G_N$$G_1,G_2,...,G_N$: the regions of safe terrain, represented as convex polytopes

$\mathbf{Y}\in \{0,1{\}}^{R\times N}$$\mathbf Y \in \{0,1\}^{R\times N}$: assignment of footsteps to safe regions

Thus, the optimization problem is:

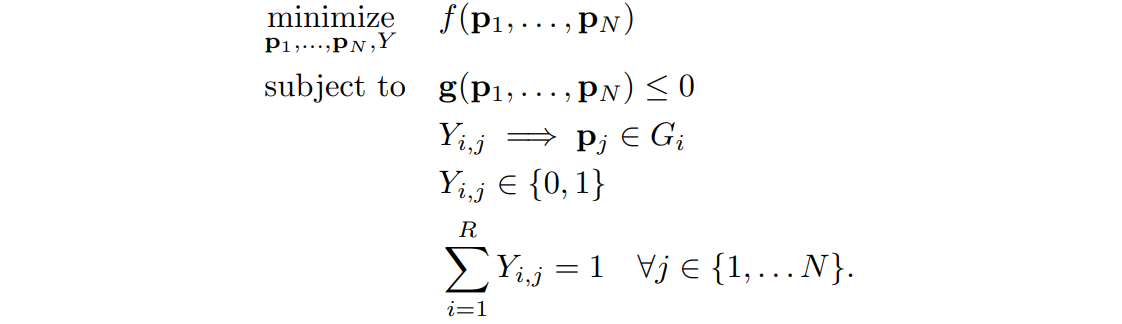
3.1.1 Convex Decomposition (regions of safe terrain)

Require: minimize the number of convex pieces and focus on creating large convex regions

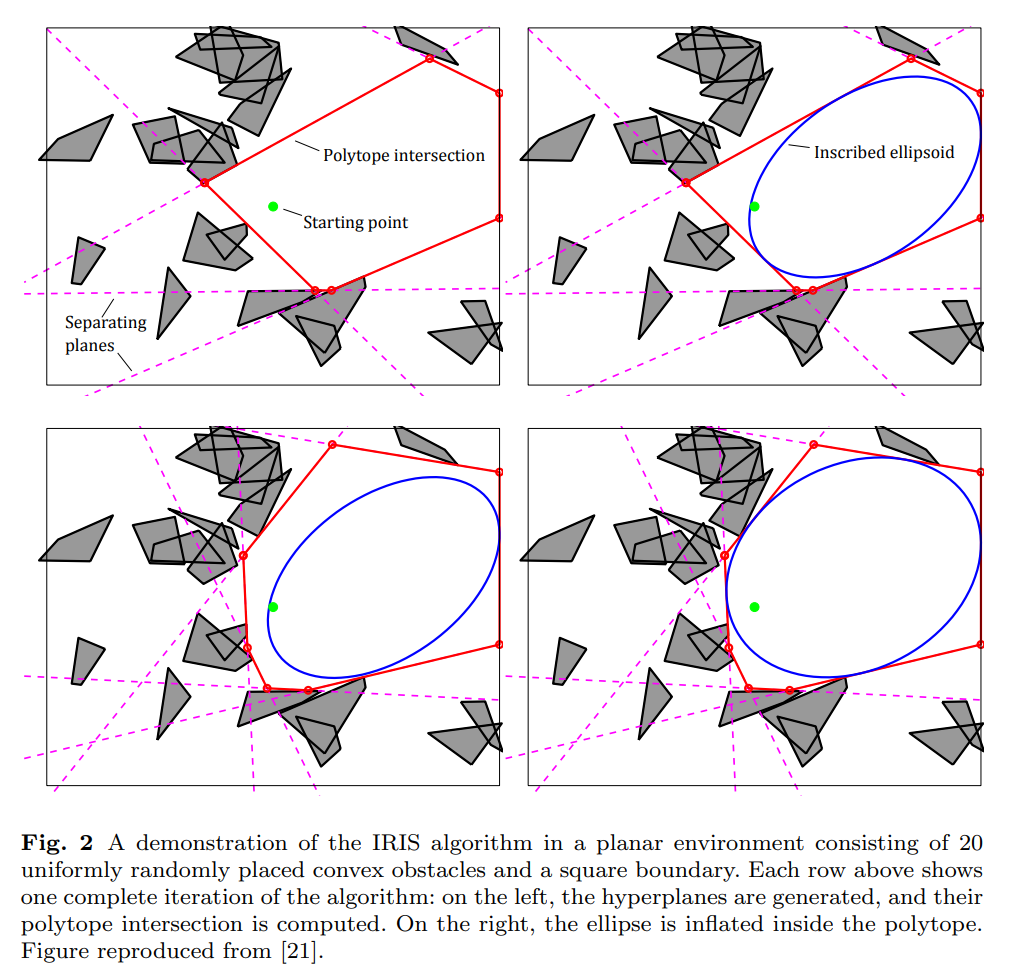
Developed IRIS^[21], an algorithm for greedily computing a single large obstacle-free convex region

IRIS begins with a seed point that is known to be obstacle-free, and alternates between two convex optimizations, such point is currently provided by human pilot.

Repeat following 2 steps to grow the ellipsoid until a local fixed point is found:

1. a series of small quadratic programs are solved to find a set of hyperplanes that separate the ellipsoid from the set of obstacles. Each hyperplane defines an obstacle-free half-space, and the intersection of those half-spaces is a (convex) polytope
2. a single semidefinite program is solved to find the maximum-volume ellipsoid inscribed in that polytope

This paper uses the polytope as obstacle-free space, since it is always larger and can be represented as a set of linear constraints

3.1.2 Representing Reachability (poses of the footsteps)

full kinematic model of the robot $⟹$$\Longrightarrow$ polynomials of trigonometric functions of the robot’s joint angles

This work represents the approximate reachable set of footstep positions as the intersection of circles fixed in the frame of reference of the prior footstep.

Each circle has radius $d_k$$d_k$ and is located at some fixed offset $o_k$$o_k$ in the frame of the prior footstep. In order to avoid the non-convexity introduced by sin and cos, Fig. 3 can be represent as follows:

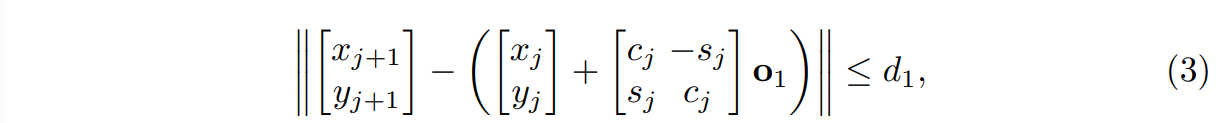
where : $s_j\equiv \sin {\theta }_j$$s_j\equiv\sin\theta_j$ , $c_j\equiv \cos {\theta }_j$$c_j\equiv\cos\theta_j$ , then create piecewise linear approximations of sin and cos.

Alternatively, fix the yaw angle of each footstep beforehand, then run the mixed-integer optimization to determine the position and assignment to safe terrain for each footstep

To alternate between the following 2 steps could further refine the footstep plan: (may remove any guarantees of global optimality, but still produce acceptable footstep plans)

1. using a nonlinear optimization to choose the footstep orientations
2. running the mixed-integer convex optimization to choose the optimal position and assignment of those footsteps at the given orientations

When the environment is cluttered, however, the full mixed-integer convex optimization discussed above is required in order to find feasible solutions.

3.1.3 Determining the Number of Footsteps

Add a binary flag to each footstep to indicate that the particular step is unused

${\rho }_j$$\rho_j$: if true, then footstep $j$$j$ be fixed to the starting pose of that foot

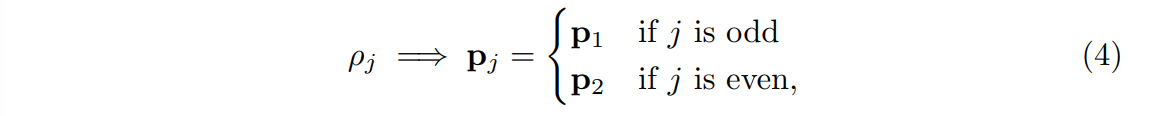
To minimize number of footsteps $⟹$$\Longrightarrow$ Adding a negative cost on each ${\rho }_j$$\rho_j$ to the objective in our optimization

DEFINE

${\mathbf{p}}_g\in {\mathbb{R}}^4$$\mathbf p_g \in \mathbb R^4$: goal pose

${\mathbf{Q}}_g,{\mathbf{Q}}_r\in {\mathbb{S}}_{+}^4$$\mathbf Q_g,\mathbf Q_r \in \mathbb S^4_+$: objective weights on the distance to the goal and between steps

$q_t\in \mathbb{R}$$q_t \in \mathbb R$: objective weight on trimming unused steps

${\mathbf{p}}_{min},{\mathbf{p}}_{max},\mathrm{\Delta }{\mathbf{p}}_{min},\mathrm{\Delta }{\mathbf{p}}_{max}\in {\mathbb{R}}^4$$\mathbf p_{min},\mathbf p_{max}, \Delta \mathbf p_{min}, \Delta \mathbf p_{max}\in \mathbb R^4$: bounds on the absolute footstep positions and their differences

${\mathbf{p}}_1,{\mathbf{p}}_2$$\mathbf p_1, \mathbf p_2$: initial poses of the robot’s feet

$g_{s,l},h_{s,l},g_{c,l},h_{c,l}$$g_{s,l},h_{s,l},g_{c,l},h_{c,l}$: pre-selected piecewise linearization of the sine and cosine functions, see [22]

Then formulate the entire footstep planning optimization as follows:

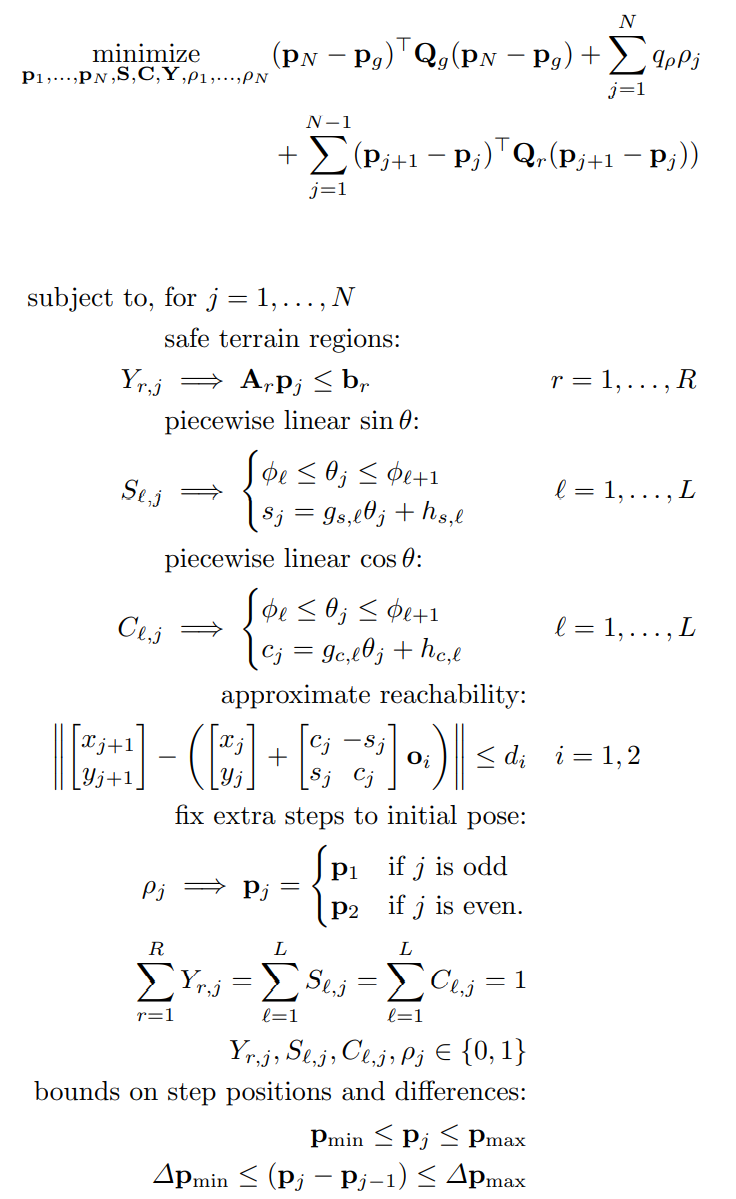
3.2 Dynamic Motion Planning

DEFINE

$\mathbf{q}$$\mathbf q$: generalized position

$\mathbf{v}$$\mathbf v$: velocity

$\mathbf{k}$$\mathbf k$: centroidal angular momenta

$\mathbf{l}$$\mathbf l$: linear momenta

${\mathbf{A}}_G$$\mathbf A_G$: centroidal momentum, the total momentum defined in a coordinate frame at the instantaneous center of mass (COM)

$\mathbf{r}$$\mathbf r$: COM of the robot

$m$$m$: total mass

$\mathbf{g}$$\mathbf g$ :the acceleration due to gravity

${\mathbf{c}}_j,{\lambda }_j$$\mathbf c_j , \mathbf \lambda_j$ : the contact position and force at point j

$N_c$$N_c$: number of active contact points

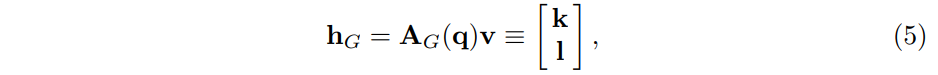
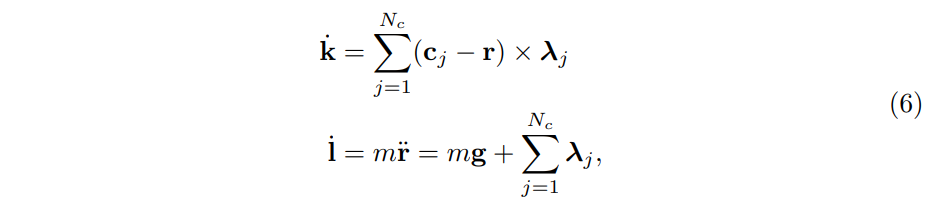
There has been compelling recent work in controlling the momenta of humanoids for balance and locomotion [40, 45, 32, 38], including the resolved momentum control framework proposed by Kajita et al. [37, 53].

Assuming the robot’s $(n-6)$$(n-6)$ internal degrees of freedom are fully actuated, and that the dynamic constraints can therefore be defined in terms of the 6 floating base DOFs (will be unable to reason about internal torques)

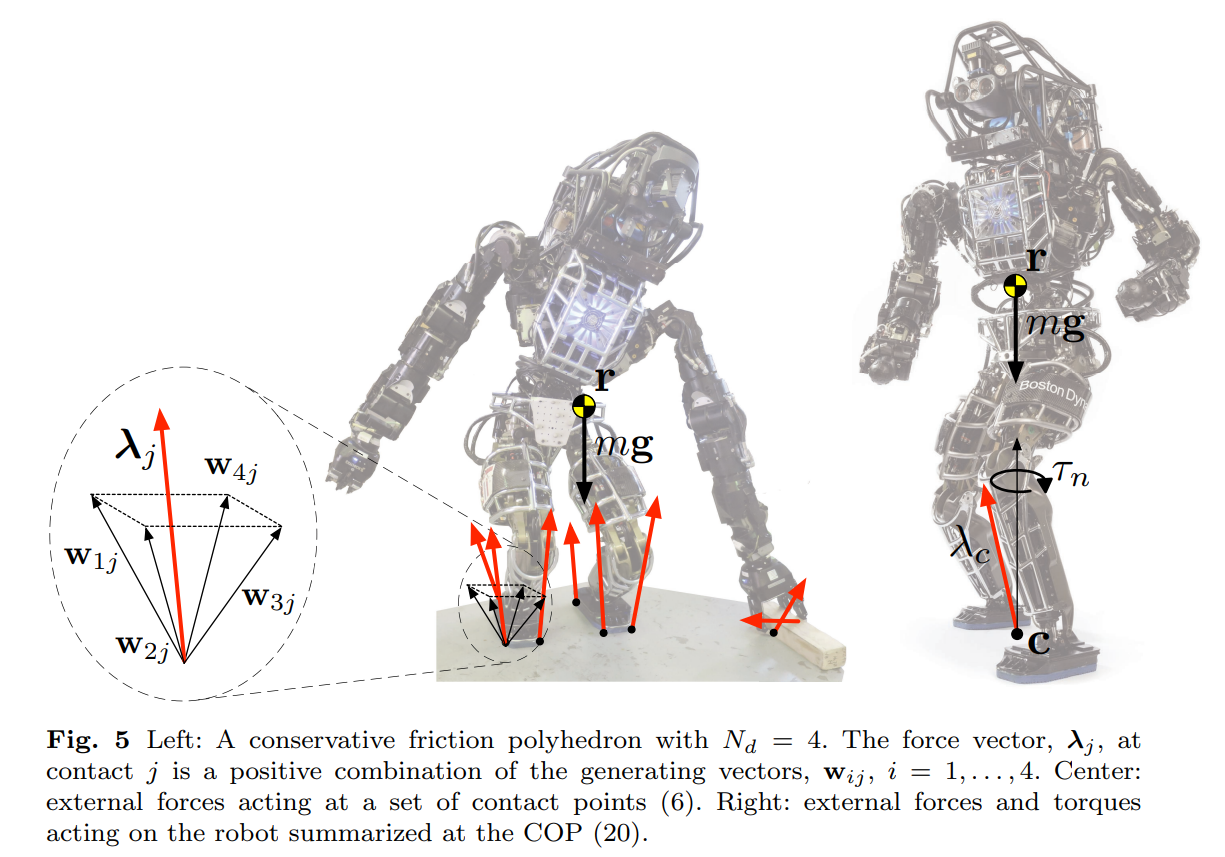
Use a friction cone for each active contact point:

where:

${\mathbf{n}}_j$$\mathbf n_j$: the contact-surface normal ${\mathbf{d}}_{ij}$$\mathbf d_{ij}$: i-th tangent vector for the j-th contact point ${\mathbf{w}}_{ij}={\mathbf{n}}_j+{\mu }_j{\mathbf{d}}_{ij}$$\mathbf w_{ij}= \mathbf n_j +\mu_j \mathbf d_{ij}$: the generating vectors ${\mu }_j$$\mu_j$: the Coulomb friction coefficient $N_d$$N_d$: the number of tangent vectors used in the approximation

The 2 major trajectory optimization algorithms:

1. Shooting methods involve only the control inputs as decision variables and must simulate the system forward in order to evaluate the cost function
2. Transcription methods include a finite set of states along the trajectory as decision variables and incorporate the dynamics of the system as constraints on the state and input variables. By simultaneously optimizing the states and inputs along the trajectory, transcription methods avoid numerical issues that can be present in shooting methods

Similar constraint sets have been employed to control whole-body humanoid motions previously [59, 19]. Dalibard et al. [19] separately solve the kinematic planning problem using full body model and a point mass dynamic model.

4 Controller Design