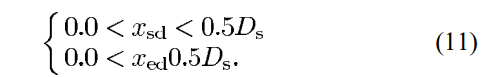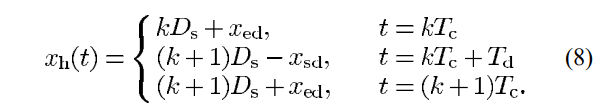Home / Research Notes / Note 1: Planning Walking Patterns for a Biped Robot

Planning Walking Patterns for a Biped Robot

by Qiang Huang et al, 2001 Paper Link

summarized by Peijie Xu

0. Abstract

1. Introduction

This paper describes a proposed method for planning walking patterns, which includes the ground conditions, dynamic stability constraint, and relationship between walking patterns and actuator specifications.

2. Walking Cycle

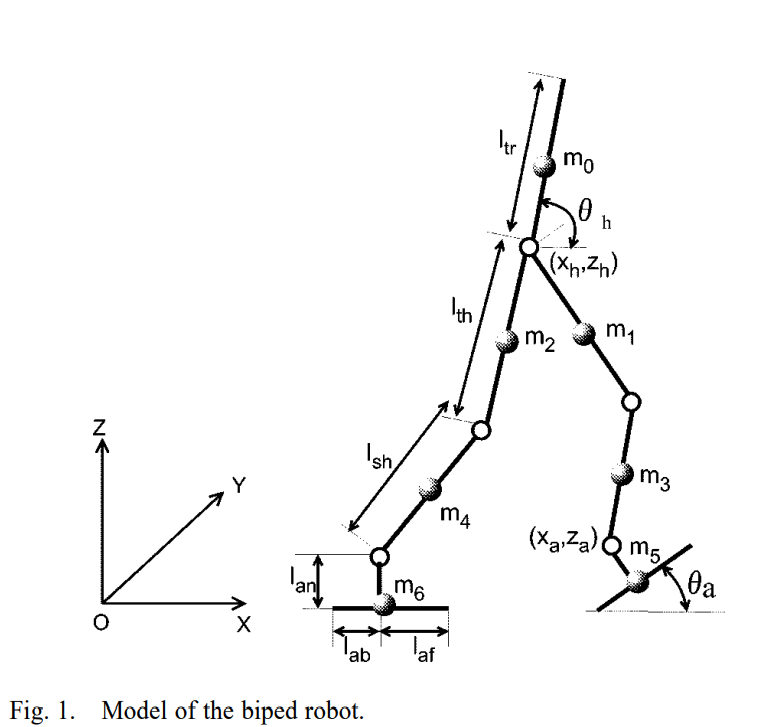
The Target Biped Robot

The humanoid biped robot with a trunk, which has 6 DOF: 3 in hip, 1 in knee, and 2 in ankle.

Biped Walking Definition

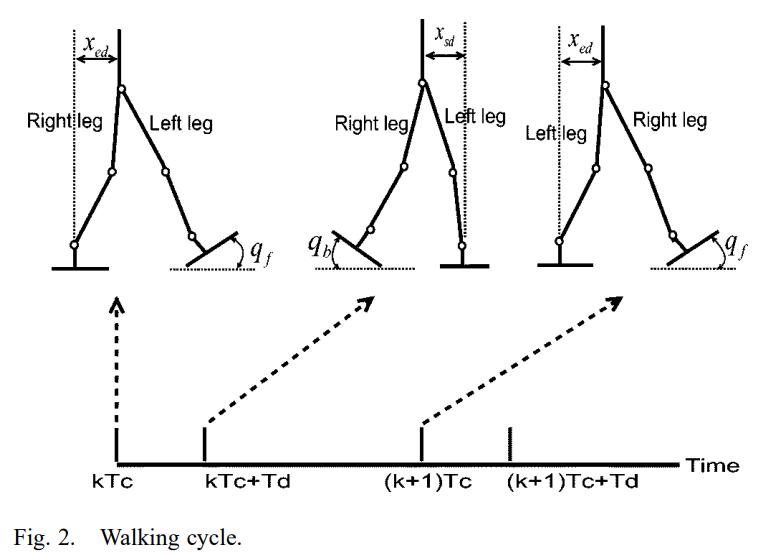
Biped walking is periodic, which is composed of 2 phases, listed below:

The interval of the double-support phase in human locomotion is about 20%, the author use this value as the basis of following calculation.

Assumption

The walking pattern can be denoted uniquely by both foot trajectories and the hip trajectory.

When the robot moves straightforward, the lateral positions of both feet are constant. The lateral hip motion can be obtained similarly as the sagittal hip motion as discussed in Section IV.

In the following sections, only discuss trajectories in the sagittal plane.

DEFINE

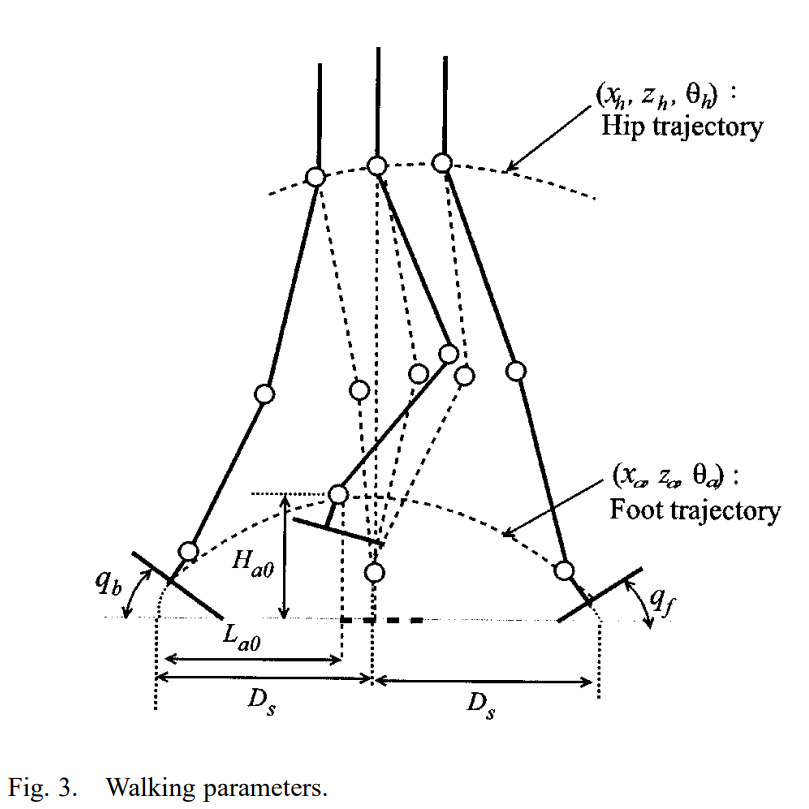
For a sagittal plane (see Fig 1):

each foot trajectory can be denoted by a vector $X_a=[x_a(t),z_a(t),{\theta }_a(t){]}^T$$X_a=[x_a(t),z_a(t),\theta_a(t)]^T$, where $(x_a(t),z_a(t))$$(x_a(t),z_a(t))$ is the ankle position, ${\theta }_a(t)$$\theta_a(t)$ is the angle of the foot

hip trajectory can be denoted by a vector $X_h=[x_h(t),z_h(t),{\theta }_h(t){]}^T$$X_h=[x_h(t),z_h(t),\theta_h(t)]^T$, where $(x_h(t),z_h(t))$$(x_h(t),z_h(t))$ denotes the coordinate of the hip position and ${\theta }_h(t)$$\theta_h(t)$ denotes the angle of the hip

We need first specify both foot trajectories, then determine the hip trajectory.

3. Foot Trajectories

In the following, only discuss the generation of the right foot trajectory, with 6+1 constraints.

DEFINE

$T_c$$T_c$ : the period of 1 walking step

$k{T}_c$$kT_c$ ~ $(k+1)T_c$$(k+1)T_c$: time of $k$$k$ th step

k th walking step (see Fig 2): begin with the heel of the right foot leaving the ground, end with the heel of the right foot making first contact with the ground

$q_b$$q_b$ and $q_f$$q_f$: angles of the right foot as it leaves and lands on the ground

Ankle Constraints

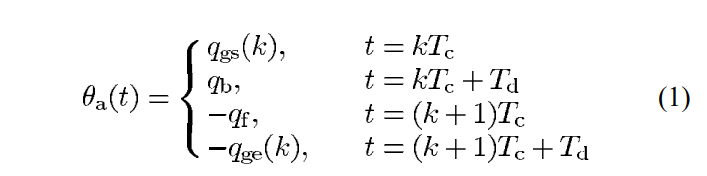
where

$T_d$$T_d$ is the interval of the double-support phase,

$q_{gs}(k)$$q_{gs}(k)$ & $q_{ge}(k)$$q_{ge}(k)$ are the angles of the ground under the support foot

Kinematic Constraints

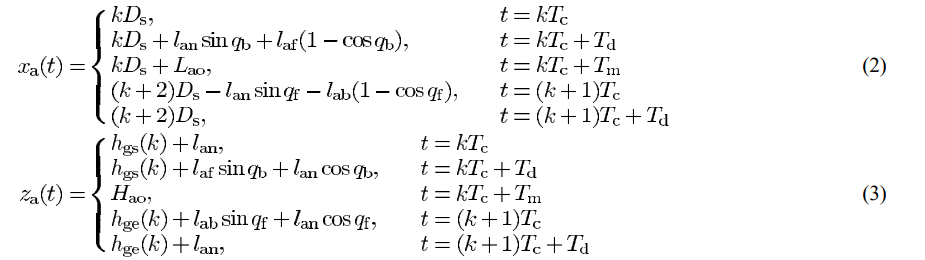
where

$(L_{a0},H_{a0})$$(L_{a0},H_{a0})$ is the position of the highest point of the swing foot (to avoid obstacles)

$D_s$$D_s$ is the length of one step,

$k{T}_c+T_m$$k T_c+T_m$ is the time when the right foot is at its highest point,

$l_{an}$$l_{an}$ is the height of the foot,

$l_{af}$$l_{af}$ is the length from the ankle joint to the toe,

$l_{ab}$$l_{ab}$ is the length from the ankle joint to the heel,

$h_{gs}(k)$$h_{gs}(k)$ and $h_{ge}(k)$$h_{ge}(k)$ are the heights of the ground surface which is under the support foot

Foot Constraints

When $t=k{T}_s$$t=k T_s$ and $t=(k+1)T_c+T_d$$t=(k+1)T_c+T_d$, the entire sole surface of the right foot is in contact with the ground

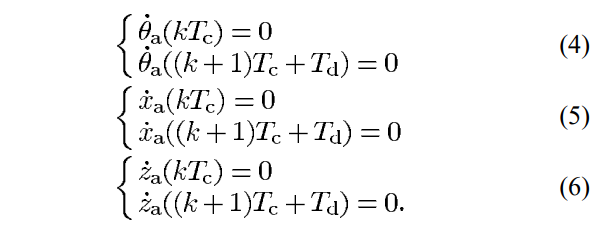
Smooth Constraints

A smooth trajectory also requires $x_a(t),z_a(t),{\theta }_a(t)$$x_a(t),z_a(t),\theta_a(t)$ to be 1st order differential and 2nd order continuous at all time.

Obtain the foot trajectory using 3rd-order spline interpolation

4. Hip Trajectory

A complete walking process is composed of three phases:

1. a starting phase in which the walking speed varies from zero to a desired constant velocity,
2. a steady phase with a desired constant velocity, and
3. an ending phase in which the walking speed varies from a desired constant velocity to zero.

${\theta }_h(t)$$\theta_h(t)$ Assumption

${\theta }_h(t)$$\theta_h(t)$ is constant when there is no waist joint (at value of $0.5\pi$$0.5\pi$ rad)

$z_h(t)$$z_h(t)$ Constraints

Hip motion $z_h(t)$$z_h(t)$ hardly affects the position of the ZMP, thus specify $z_h(t)$$z_h(t)$ to be constant, or to vary within a fixed range

Assuming $H_{h,min}\le z_h(t)\le H_{h,max}$$H_{h,min} \leq z_h(t) \leq H_{h,max}$ (max at the middle of the single-support phase, min at the middle of the double-support phase)

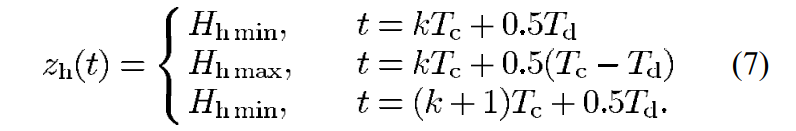
Peijie:

the middle of the single-support phase should be $t=k{T}_c+0.5(T_c+T_d)$$t=k T_c+0.5(T_c+T_d)$

Should also satisfies the 2nd order continuity

$x_h(t)$$x_h(t)$ Derivation

2 steps:

1. generate a series of smooth $x_h(t)$$x_h(t)$;
2. determine the final $x_h(t)$$x_h(t)$​ with a large stability margin.

Step 1: obtain a series of smooth $x_h(t)$$x_h(t)$

DEFINE

$x_{sd}$$x_{sd}$ & $x_{ed}$$x_{ed}$ : distance at the start and end of the single-support phase (see Fig. 2)

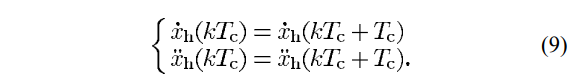
to obtain a smooth periodic $x_h(t)$$x_h(t)$, as well as the 2nd derivative continuity conditions, the following derivative constraints must be satisfied:

the $x_h(t)$$x_h(t)$ can be derive:

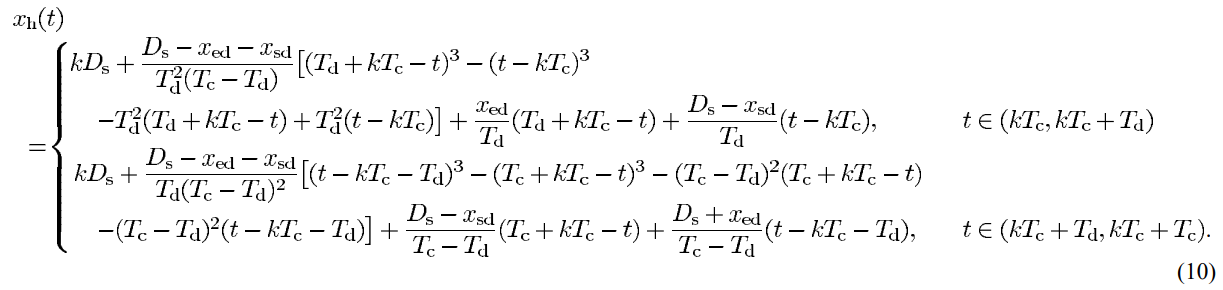
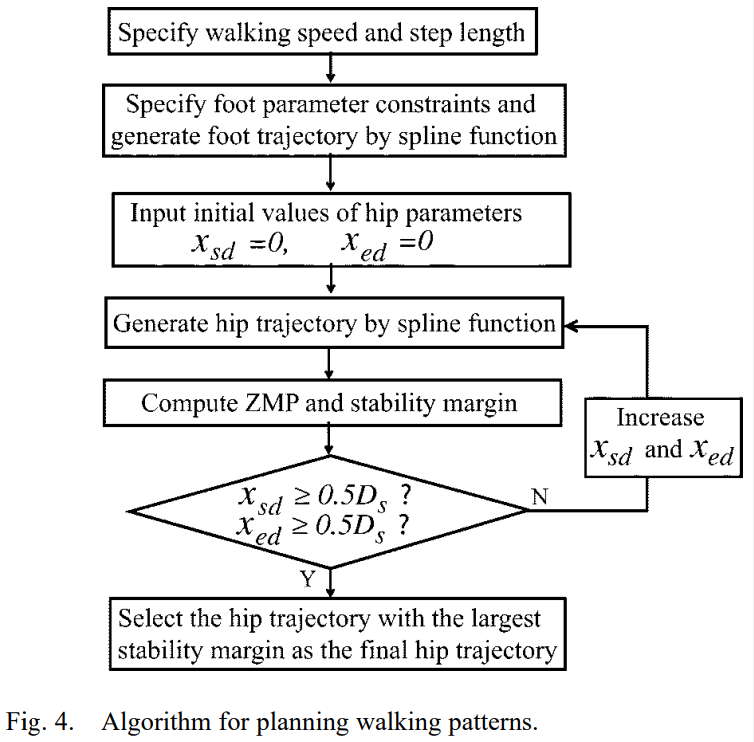
Step 2: determine $x_h(t)$$x_h(t)$ with largest stability margin

a smooth trajectory with the largest stability margin can be formulated as follows:

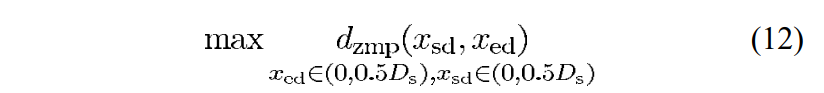
the algorithm to solve it:

at the start and end, velocity should be 0